Sound
Sound is the perceived complex phenomenon of vibrations traveling as pressure waves through a medium. For all living beings on earth this medium is either air or water. Such vibrations are called sound when they are perceived by (our) hearing.
There are thus three components in sound: vibration, medium, hearing. Generally, silence is considered to be the opposite of sound.
In music, silence is always relative to sound and sound volume, just as in visual art darkness is relative to light and lightness.
Parameters of sound
A musical sound can be recognized and defined by its pitch (or frequency), duration (or relative rhythmic value), timbre (color or instrument), dynamics (loudness) and position in space (relative to the listener)1. These musical parameters furthermore include the following concepts when applied to groups of sounds: register position(s), density, color palette, general loudness level(s) and spatial distribution(s). All music consists of related sounds and silences, which can be symbolized by notation.
Hearing
Sound is perceived by our hearing, which is a result of our ears picking up vibrations in the air and translating these to our brain, where the perception of hearing comes to awareness2.
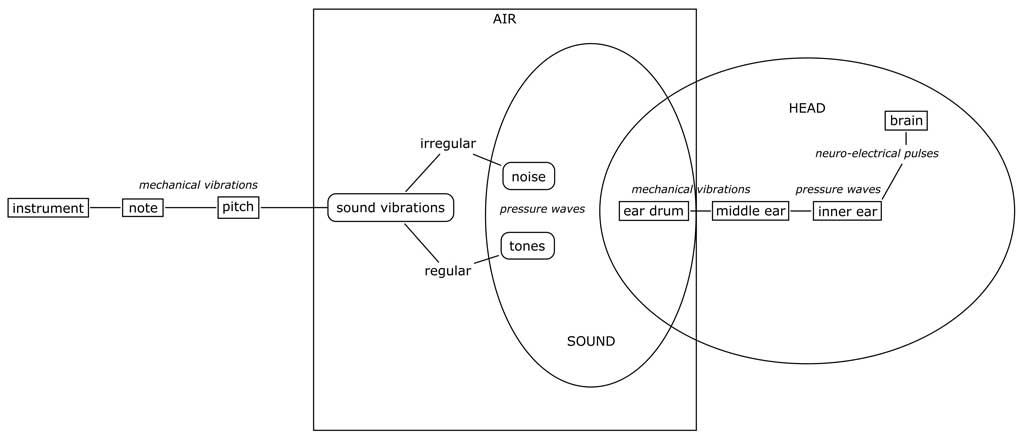
The ear translates vibrations in the ear into neural signals. Air-vibrations are received by the ear drum (tympanic membrane) and transmitted by means of the three extremely small bones called ossicles (as the fossil record shows, these originally evolved from jaw bones hundreds of millions of years ago), whose intricate lever-function is to reduce the amplitude of the vibration while increasing the energy transmitted, to the inner ear (labyrinth). The middle ear thus translates pressure waves (back) into mechanical vibrations. The inner ear serves two functions, those of hearing and of balance. The cochlea is the coiled part of the inner ear which translates the mechanical vibrations into pressure waves in its internal fluid, which are picked up by hair cells that convert their motion into electrical signals. These are in turn interpreted by nerve cells that transform them into electrical impulses that travel through the auditory nerve to structures in the brainstem for further processing. Hearing is a complicated mechanism!
Physics of sound
A tone is a complex combination of a series of regular vibrations, usually with one prominent frequency which is experienced as the pitch. A regular vibration is scientifically named a frequency, expressed in Hz (Herz), cycles per second.

The amplitude of such a wave corresponds directly to the volume of a sound, the wavelength to its pitch, or frequency. Standard tuning in music today is usually to A=440Hz45 which means there are 440 vibrations per second to produce this tone. Although human hearing ranges between 25 to 20,000 Hz, the pitches actually used in music are roughly between 25 and 5,000 Hz.
Ultrasound, sound too high for human perception, is used by animals such as dolphins6, bats7 and mice.8
Infrasound, sound too low for human perception9, is found in larger animals such as hippos, elephants10 and whales11.
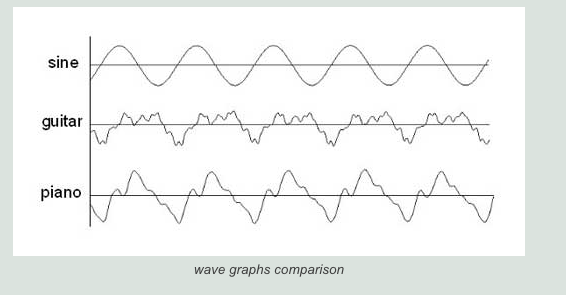
The basic regular vibration is a sine-wave, but all musical instruments actually produce a combination of various sine waves for each tone. Differences in these combinations are perceived as various colors of sound. Some examples of oscillograms are given below.
Most animals have a very different hearing (and correspondingly: sound producing) range from us humans. For example, elephants and whales hear and communicate with subsonic frequencies (infrasound) over vast distances, whereas bats and dolphins use a sonar system employing extremely high frequencies (ultrasound) to locate their prey at short range, especially in conditions where sight will not avail them12.
Various tones overlapping or sounding together will produce generations of audible combination tones in the inner ear, sum- and difference tones coming from the interference of their compound frequencies, producing complex harmonies and tensions between different tones, described by the subjective concepts consonance and dissonance.
Musical notation
- Musical notation is used to write or print sheet music for performance.
In a strict sense the words note and tone do not have the same meaning. Both can be notated, but a note is notated by its shape, and a tone by its vertical position on a staff. A note indicates a time value of relative duration, a tone indicates a pitch, a stable frequency of sound. Although musical notation uses both at the same time: notes are needed to notate rhythm, as tones are needed to notate melody and harmony.
Note and rest values
- A note is the relative rhythmical value of a duration of a sound.
- A rest is the relative rhythmical value of a duration of a silence.
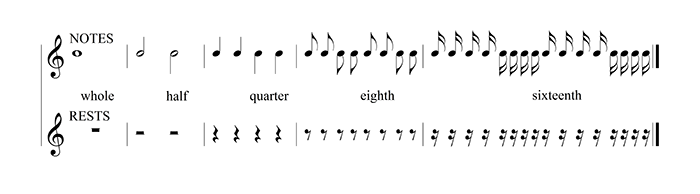
Most written or printed music today makes use of a small set of notes, ranging from the whole note to the 1/16 note. To indicate silence, a set of corresponding rests exists as well.
The system of notation of durations works by double and half values. Two 1/2 notes or rests, add up to the same duration as a whole note or rest (two rests add up to a longer silence, but two notes generally mean two sounds, so it is not always identical); two 1/4 notes add up to the same duration as a 1/2 note; two 1/8 notes add up to the same duration as a 1/4 note; two 1/16 notes add up to the same duration as a 1/8 note; see and hear example 1 which compares and demonstrates this:
In the example above, alternate directions are notated in the notestems, half of them are notated upwards and half downwards, and this suggests some grouping. Normally, stem directions depend on the position of a note on a staff: when it is high, the stem goes down, when it is low, the stem goes up. To more clearly show the rhythmical groupings, notes are always beamed together per beat, this means that the values flags are written as horizontal lines, as in the example below. In example 2, the exact same order is notated as before, but now graphically improved for reading:
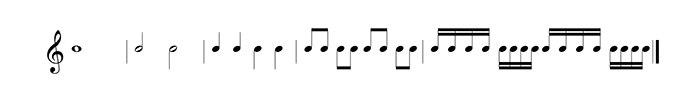
Notation of time and rhythm
Symbols for notes and rests
To represent different durations of tones, different note symbols were developed. The normal ratio of durations is 1:2, each smaller, faster note being twice as fast, or: half as long, which amounts to the same result, as the larger one. The system begins with the whole note. The smaller values then are the half note, quarter note, eighth note, etc., always halving the previous value. Older terms for these note symbols are still in use in some countries, such as “quaver”, “semi-quaver” and “crotchet”, but I consider these to be both confusing and outdated, so I prefer to use the numerical values and names.
Nevertheless, a simple table comparing both systems of naming is given here:
| International numerical nomenclature | Traditional nomenclature |
| whole note (1) | semibreve |
| half note (1/2) | minim |
| quarter note (1/4) | crotchet |
| eighth note (1/8) | quaver |
| sixteenth note (1/16) | semiquaver |
| thirty-second note (1/32) | demisemiquaver |
| sixty-fourth note (1/64) | hemidemisemiquaver |
| one hundred and twenty-eighth note (1/128) | quasihemidemisemiquaver |
Below are the notation symbols for most of these values:
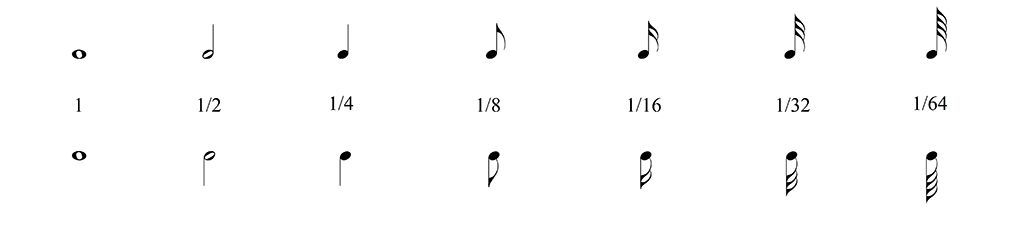 note values
note valuesA similar system of symbols with relative durations is used for musical silences, called pauses or rests.
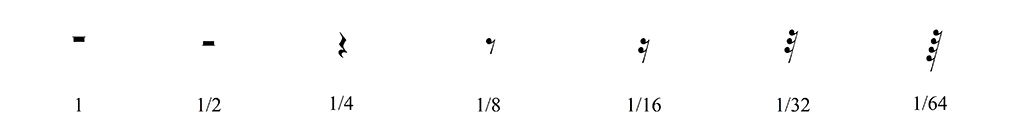 rest values
rest valuesThe whole rest can be used for two purposes:
- A true whole rest, with the exact value of a whole note;
- A full bar rest, not literally corresponding to and therefore independent of time signature.
Time signature and bar
A time signature consists of two numbers, one above the other, without a horizontal line between them (it is not a fraction). The upper number indicates the number of beats, the lower number represents the note value used for one beat. Although time signatures using the quarter or eighth notes as basis are more common, theoretically many more are possible, and indeed sometimes used.
The most common time signatures are two-four, three-four, four-four and six-eight. Eighth and smaller notes can now be grouped and visually linked together per beat. In grouping these smaller note-values thick horizontal lines, called beams, are employed. These are double beams in the case of sixteenth notes, triple beams with thirty-second notes, etc. It is also possible to thus beam together notes of different values, as long as the beamed groups are a clear representation of the beat-structure. Further details on beaming will be explained later in this outline.
With the use of time signatures, the notes become grouped in units called bars or measures, each group separated from the next by a vertical line, called the barline.
Any grouping of notes that is more complex than the time signature within it is notated represents a rhythm. Meter itself may be considered a rhythm, a simple rhythm, but rhythm is generally not a meter.
A longer sequence of rhythmical values may constitute a phrase.

Basic tempo indication
Basic tempo indications are done with the one-beat note-value, an = sign and the number of beats per minute (also called bpm). The example above could then be notated in the following way, to produce three times the exact same rhythm, because of the tempo and counting adjustments notated:

Note that when changing the one-beat note, the equals sign = actually means becomes.
More on tempo indications can be found in the section on other notation symbols.
Alteration
Definition of alteration
Alteration in music is the changing of a basic tone, by raising or lowering it’s pitch with one or two semitones or other microtones; opening up possibilities of alteration is the first step in the direction of a chromatic system.
Symbols for alteration
In notation the following signs are used for this:
- Sharp, to raise the pitch by one semitone;
- Flat, to lower the pitch by one semitone;
Melody
Definition of melody
Melody is created by a sequence of different single pitches in time.
Harmony
Definition of harmony
Harmony is created by the interrelationships of different pitches together in time; the timing of the sounds used, called harmonic rhythm, is an ingredient as essential as the sounds themselves!
Functional harmony
Whereas harmony in general is a concept which describes the relative sounds of large groups of tones, the term functional harmony is used for a specific, yet generally used, type of harmony, generating the expectation of a central tone or chord, called the tonic, by means of tension and resolution.1
Functional harmony rests on three pillars, called functions:
- Tonic: a “home” sound or chord, a resting place within the progression of chords
- Dominant: a point of maximum tension relative to home, the “going home” chord, creating expectations of resolution
- Subdominant: an alternative resting place, though not “home”, but rather perhaps an “out, on a holiday” chord, anything can happen after this
Functional harmony can create story-like structures in time with these elements, relatively easy to hear and follow, even for non-trained ears.
Not all harmony is functional! Harmony can also be non-functional, in which case the expectation of a tonic is absent, even though an harmonic focus can be present. Among non-functional harmony there exist such phenomena as modal harmony, parallel harmony, and atonality.
Definition of degree
A degree is a harmonization of a particular scale-step, indicated by a Roman numeral.
A degree exists in relation to an audible functional harmonic center, called the Tonic, symbolized by a I. Relative to this I, other degrees are numbered around it. If another degree than the I forms a temporary harmonic center, this is created by at least one Secondary degree, usually a Dominant sometimes accompanied by a Subdominant degree.
Degree as chord
Any scale can be harmonized by forming triads, seventh- or other chords on its steps. The harmony thus obtained is proper to that particular scale itself and can be modal or tonal, depending on its use.
Mostly, degrees are formed by a construction of thirds, but this can also be done with other intervals.
Degree as scale
New scales or modes can be derived from any particular scale, by using the scale on a degree of another scale. Thus the church modes, the harmonic minor modes and the melodic minor modes can be found, but one could also imagine this method as a starting point for harmonizing very different modes still, such as a Carnatic raga or a Turkish makam.
Basic degrees as triads
Degrees can be shown as part of a circle of degrees:
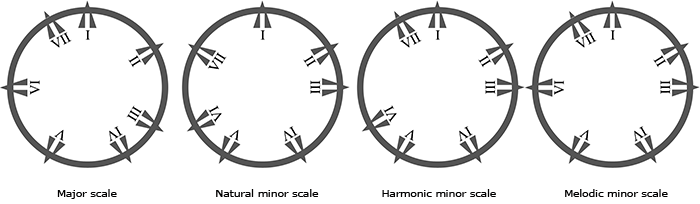
This modal approach does not always correspond to the functional tonal use of degrees, but does enlarge the number of possibilities. In such a way, modal elements can be added to tonal music.
We shall proceed however with the most basic triads, occurring not on the scales, but rather in the keys of, major and minor.
Basic degrees in major
The basic major scale (in c consisting of basic tones) generates the degrees given below.

Basic degrees in minor
The basic degrees used in minor are given below (example in c minor) :

Circle of fifths
Major scales in order of accidentals
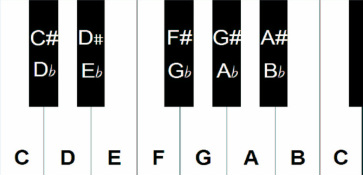
It is possible to construct a major scale on every tone, and different accidentals are needed to induce the proper order of steps: whole, whole, half in both tetrachords (4 tone scale part). Without use of accidentals, only the scale of c major yields this strucure in both tetrachords: both c d e f and g a b c share this structure: 1 1 ½. These tetrachords are both connected to the fundamental c, the first has it as lowest, the second as highest note. The remaining interval f g is a consequence of this tetrachordal construction, and in itself a whole step (major second). The total scale thus shows 1 1 ½ 1 1 1 ½.
When constructing this on different tones, we can set the scales we find into the following order by number of accidentals, those we find having sharps:

And those we find having flats:

If we allow for the use of double sharps and flats, more scales are possible, but for practical reasons the keys (and hence the scales) remain limited to those employing a maximum of 7 accidentals.
Minor scales in order of accidentals
It is also possible to construct a similar series when studying minor. In order to obtain similar accidentals, we use the minor-parallel or parallel minor scale, or aeolian mode, which can be found on the VI of any major scale. VI of c being the a we find the following order by number of accidentals, with sharps:

And another series yet, employing flats instead, starting with the parallel of f, d:

Key signatures in order of accidentals
Note that both orders are based upon the diatonical series of fifths we discovered earlier:
either, for the sharps
- f c g d a e b
or the reverse, for the flats
- b e a d g c f
which form a diatonic circle of fifths, as shown again in this image, that also mentions the church modes. Not all these fifths are perfect however, this diatonic circle of fifths contains one diminished fifth: f – b.
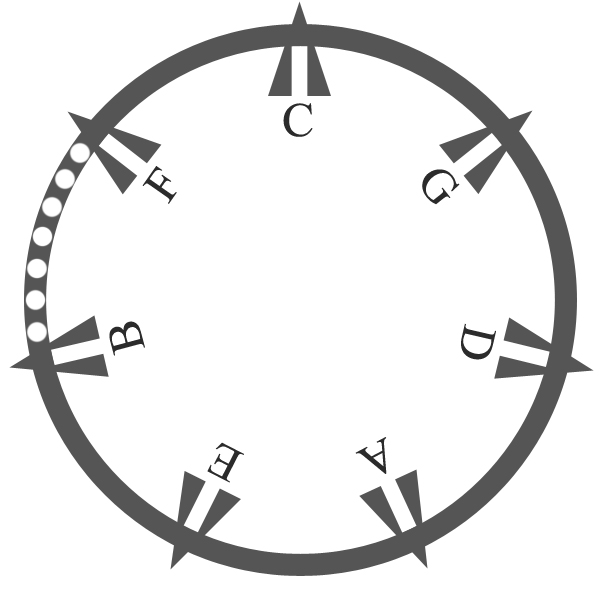
The order of appearance of sharps is fixed as:
f# → c# → g# → d# → a# → e# → b#
the example shows the correction notation of the key-signatures with sharps on two clefs:

The order of appearance of flats is also fixed and the exact reverse as to the use of basic tones:
b♭ → e♭ → a♭ → d♭ → g♭ → c♭ → f♭
the example shows the correction notation of the key-signatures with flats on two clefs:

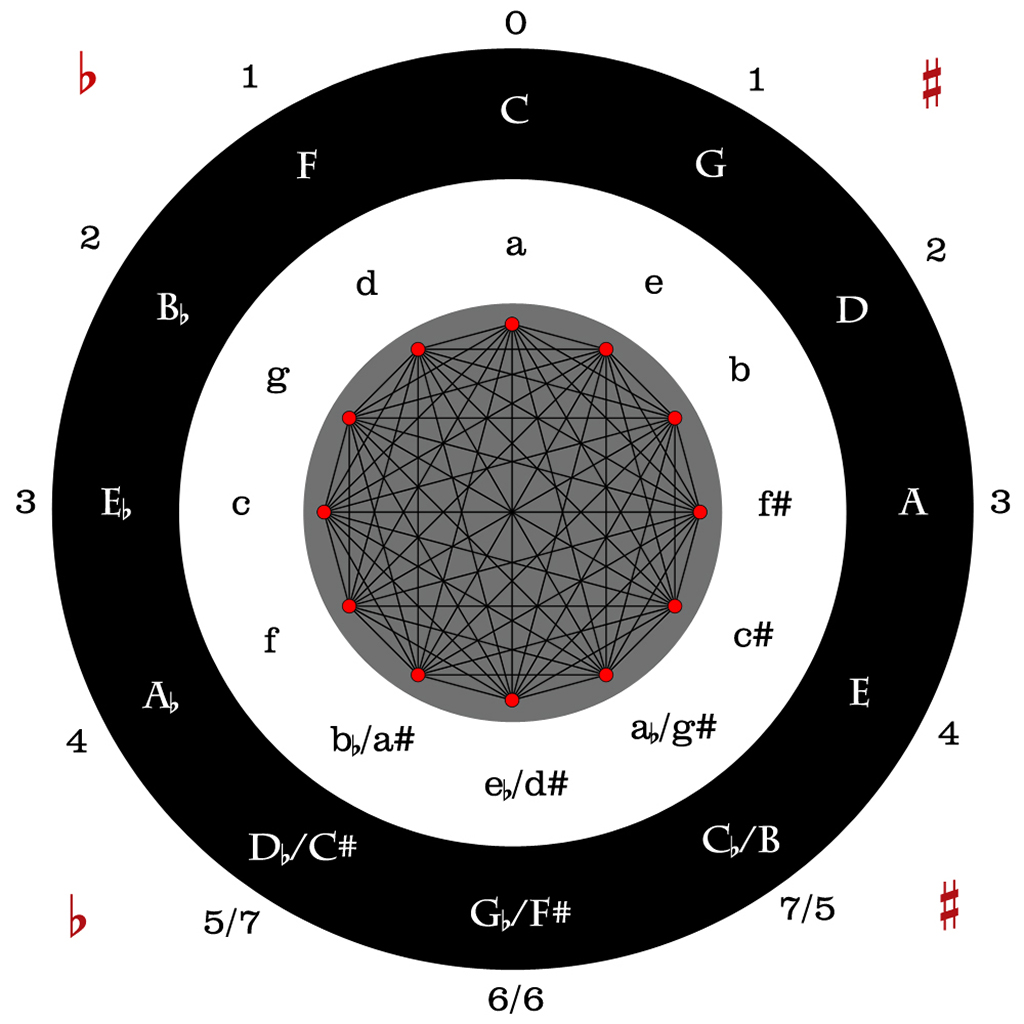
Geometry of the full circle of fifths
We can now summarize this structure and knowledge in the circle of fifths.
The image of the circle of fifths summarizes and visually represents the observations on major and minor scales and keys and the key signatures with number and order of sharps and flats, but it also allows a further geometrical look into the intervals, and their place within this representation.
Building blocks of harmony
- Harmony consists of tones sounding together in time.
There are two types of sounding together in music: simultaneous and sequential. The musical sounding together can be accomplished by both means, and both can be included in the broad concept: harmony.
Building blocks of harmony – part 1: Scales
Scales
- A scale is a set of 5 or more tones, arranged in stepwise order, spanning an octave.
The simplest way to order a set of tones is in a scale. There exist a vast number of scales, but for the purposes of this elementary course this wealth is limited to a few, to be known really well for a start.
A scale arranges tones in a stepwise order. There are different kinds of steps, varying in size, the most common we will encounter are:
- the semitone step, abbreviated by the number ½
- the whole tone step, abbreviated by a number 1
- the next larger step of 1½, either by skipping a tone or by an altered neighboring tone
Steps and scales are different in different tuning systems, this course uses the equal tempered tuning throughout. The equal tempered tuning is today used for almost all Jazz- and Pop- and most World and Classical music. Other tunings are used in World music and so-called authentic performances of Baroque, Renaissance and Medieval music. The modern equal tempered tuning has as its huge advantage that all similar steps are equal:
- In equal tempered tuning all semitone steps are the same.
Chromatic scale
The chromatic scale is the scale with only semitone distances, using all 12 tones. Ascending, it is notated with sharps, descending with flats. This facilitates reading, but also represents the musical perception of the functions of the tones mutually:
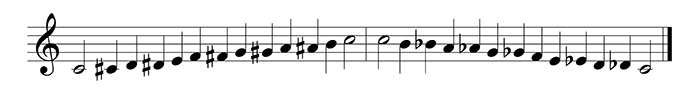
Pentatonic scales
With the material of the seven basic tones we can build the two most common pentatonic scales. The prefix penta comes from ancient Greek music theory, and means five, so: 5-tone scales. First let’s look at and listen to the major pentatonic scale of c, after listening you should sing it as well:

– pentatonic major scale
- the major pentatonic scale has 5 tones (here: c, d, e, g and a)
- the major pentatonic scale has the following structure of 5 steps: 1 – 1 – 1½ – 1 – 1½
Taking the exact same tone material, but now from a to a, we get the minor pentatonic scale of a, after listening to both these scales, practice singing them along and alone as well, keeping them well apart:

– pentatonic minor scale
- the minor pentatonic scale has 5 tones (here: a, c, d, e, and g)
- the minor pentatonic scale has the following structure of 5 steps: 1½ – 1 – 1 – 1½ – 1
You may have noticed that I have used both the terms “major pentatonic” and “pentatonic major”, and that these mean the exact same. Just the word “pentatonic” however denotes merely the 5-tone structure but does not make clear which pentatonic scale is meant.
Basic diatonic scales
The basic diatonic scales are also known by their traditional name: church modes. The definition of a diatonic scale is that it consists of only whole and half steps, nothing larger therefore. The basic diatonic scales are also called modes, which can be a more complex concept as well. In practice the word mode is often used as meaning scale, but the word mode can be used to indicate a certain use of the scale as well.
The material for the basic diatonic scales, are the seven basic tones c, d, e, f, g, a and b. Arranging these in stepwise order, spanning an octave we get 7 scales, each with its traditional name, The student is advised to become fully familiar with these scales, and singing after hearing as well as singing along is a good start, noting its overall sound (mode), the different steps, and the detailed harmonic positions of the tones compared to its fundamental tone:

– ionian
- the ionian scale or mode is also known as the major scale, and one of the 3 basic major modes
- the step structure is 1 – 1 – ½ – 1 – 1 – 1 – ½
- this downwards step order is identical to the upwards step order of phrygian
- the harmonic positions of the tones are 1 – 2 – 3 – 4 – 5 – 6 – 7
Harmonic and melodic minor scales
Above we saw the major (also: ionian) and the natural minor (also: aeolian) scales, but there are two more minor scales every musician should be familiar with.
These two scales, harmonic and melodic minor, have each a unique step structure, differing also from that of the basic diatonic scales. To distinguish them more clearly from the natural minor scale, naturals have been added in the following examples on c:

- the step structure is 1 – ½ – 1 – 1 – ½ – 1½ – ½
- the harmonic positions of the tones are 1 – 2 – ♭3 – 4 – 5 – ♭6 – 7
- this scale has a 1½ step, so strictly taken this is not a diatonic scale

- the step structure is 1 – ½ – 1 – 1 – 1 – 1 – ½
- the harmonic positions of the tones are 1 – 2 – ♭3 – 4 – 5 – 6 – 7
- consisting of only whole tones and semitones, this is also a diatonic scale
Chords
Chords
- A chord is the harmonic relationship between 3 or more tones.
A harmonic relationship is heard when tones are sounding together, which is also possible when some or all of the tones are not being played simultaneously.
Triads
- A triad is a special chord-type, consisting of three different tones, and of three intervals: two thirds and one fifth (or inversions or wide versions of just these intervals).
A triad can also contain more than three tones, by unison- or octave-doubling of the three different tones. In the following paragraphs such positions are not used; instead, simple three-note positions are presented to allow the student an overview of the underlying structures of the triads.
The basic structure of any triad can be summarized as 1 – 3 – 5
Major and minor triad
The two most commonly used chords are the major and the minor triad. Both have a perfect fifth so are considered consonant, but the difference between the two lies in the lower third (examples are all on and of c) :
- C – major chord, or major triad
- Cm – minor chord, or minor triad

Note that both perfect fifths consist of two thirds, one major and one minor third.
Triads as basic degrees in major and minor
To create basic harmony and chord progressions, scales are harmonized by constructing a triad on each scale-step, using only the tones of that specific scale. Such a triad is called a degree, and music theory indicates degrees with Roman numerals.
In this way, on the major scale, three major triads (I, IV and V), three minor triads (II, III and VI) and one diminished triad (VII) appear:


